[Disclaimer: All (or almost all) that is explained here is from the Steven and Felix Halim and Suhendry Effendy book.]
Articulation point in a graph: if you take out this node, your graph will split up in two parts ….. Bridge: the same thing would happen if you take such an edge out …..
The goal is to find such nodes or edges in an undirected graph. I have never really used this algorithm in any problem I have solved, as far as I remember :U … but it’s a fun one, like it has those moments where you go : Aaaaaaaaaaaa, that’s why :U (this thing: :U is such a mood)(I should just quit writing otherwise I will just continue jabbering and babbering about nonesense, so, let’s stop it here)
What would be the stupid way to find such vertices or edges? Just take out each node or edge one by one and check if the graph remains connected. The complexity would be O(Vx(V+E)), one is for taking out each node/edge, and the other for an algorithm to run through the graph, BFS or DFS, and check if we can access all nodes starting from one.
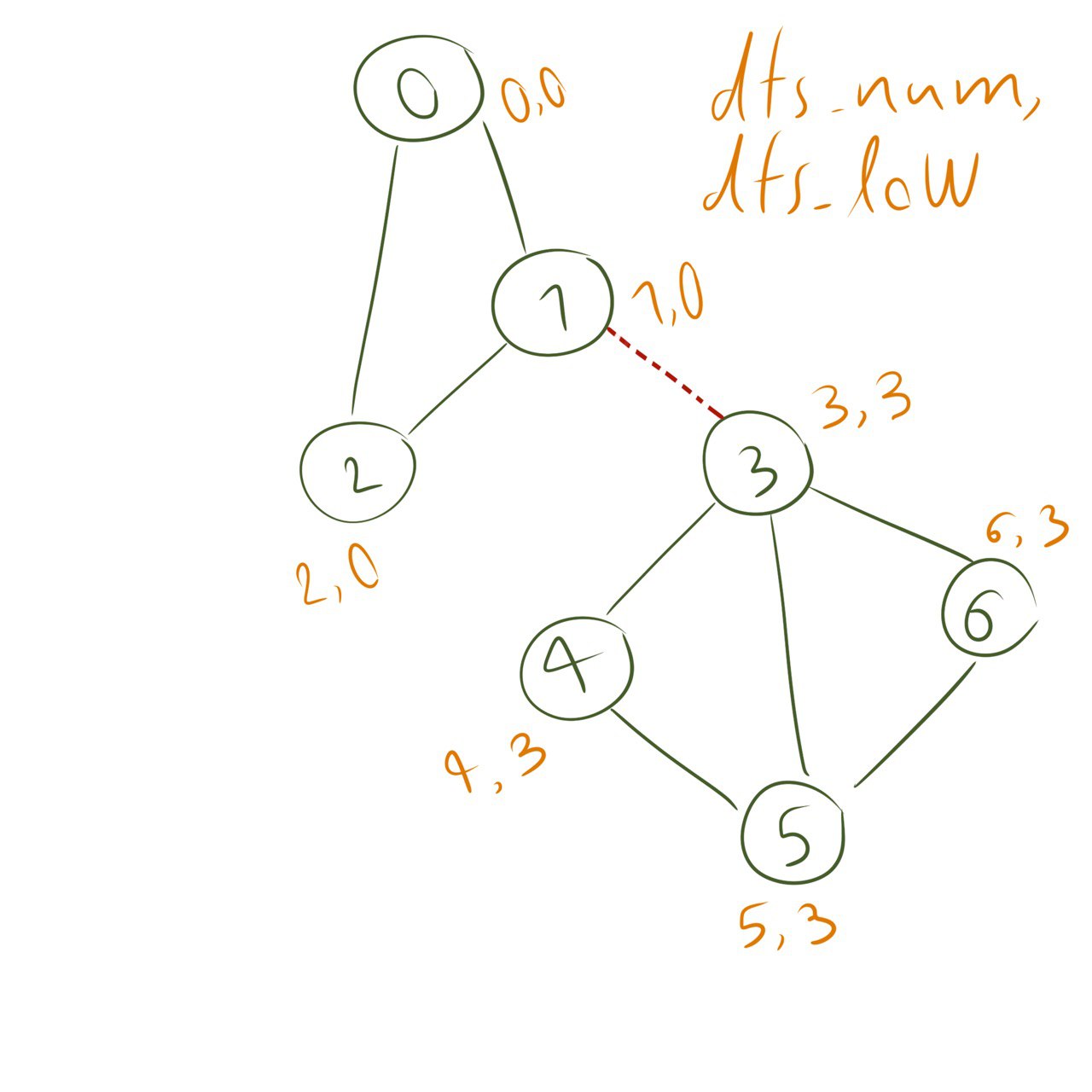
But let’s be wiser, and make some changes to DFS to make it serve our goal better; define two numbers to store for each node when applying DFS:
dfs_num : The iteration at which we visit a nodedfs_low : If R is the set of nodes in the DFS spanning subtree rooted at u, then dfs_low is the lowest dfs_num that can be found in R OR among the ones not in R but reachable by a back edge from R.
Let’s say we have done DFS over the graph and now we have all the numbers we wanted to store. consider a vertex u connnected to v, and add the condition dfs_low(v) $\geq$ dfs_num(u). What does this mean?
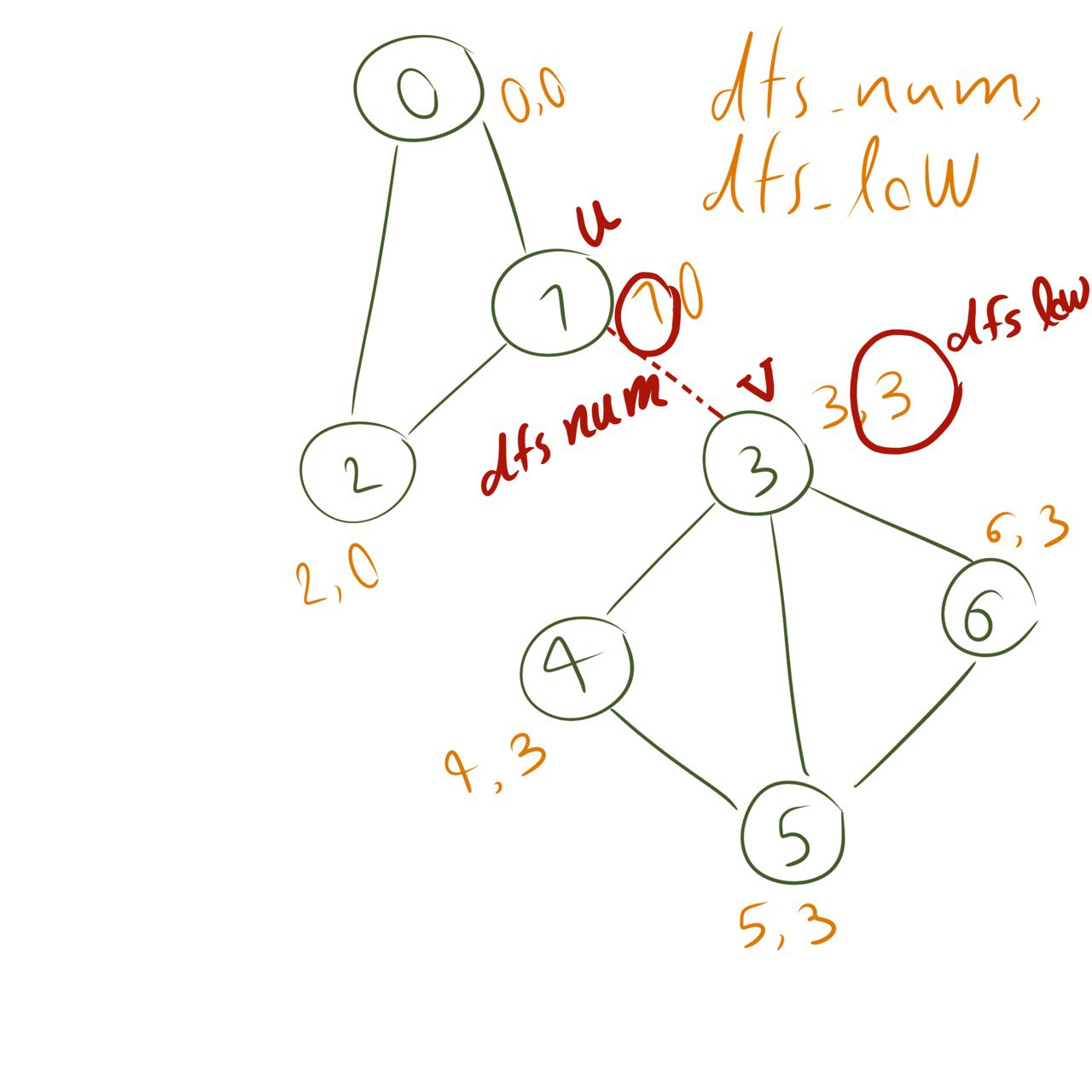
This means that we have not been able to find a lower dfs_num in the DFS subtree rooted at v or among those connected to it by a back edge. In other words, the nodes visited during DFS after visiting the node v all have higher or equal dfs_nums than that of v, which also means that there is no back edge from nodes visited in DFS after v back to the nodes visited before that point, and hence u is an articulation point! Exceptional Case: when the starting node of DFS has only one neighbor, it is obviously an articulation point; but, we cannot detectc it using the above process since it has the lowest dfs_num of all.
Detecting Bridges is similar, but the condition to check on vertices changes just a bit: dfs_low(v) $>$ dfs_num(u) . There is no equal as you can observe :U
Why?